S. M. Korobeynikov, Yu. N. Sinikh
Laboratory of Materials for Electrical Engineering
Novosibirsk State Technical University, Novosibirsk, 630092, Russia

       According to the bubble model of breakdown initiation the cause of breakdown is the bubbles of micron sizes that exist at electrodes. One managed to find optical data concerning the initiation of discharge by bubble on electrode in hexane and in nitrobenzene. In last case was used electrooptical Kerr effect that give the possibility to visualize the electric field after partial discharges and during discharge tree propagation. Several reasons of stationary bubbles existence and emergency on electrodes are discussed. The new mechanism of surface charge creation is proposed. Polar admixtures at electrodes determine the appearance of «effective» electron in the bubble at short pulses that lead to discharges in it. Emergence of surface and space charge near bubbles poles lead to bubbles deformation due to Coulomb forces. Bubble elongation causes field increase in liquid near bubble poles. Breakdown initiates in liquid phase when this field reaches critical value that depends on the liquid sample and the polarity of initiating electrode. The equation of bubble growth is computed. The basic factors that define electrical strength in model are external factors: the pressure, temperature; properties of liquid: dielectric permittivity, vapour pressure, viscosity, surface tension, density; pulse voltage parameters: the rate of pulse rise, pulse width; properties of liquid-electrode interface that determine charge injection. This performs to compute the well-known breakdown dependencies and prepare research and educational computer program.

       The key problem of breakdown is the initiation. It is undoubtedly for the cases of uniform and slight non-uniform fields due to the fact that the breakdown always must occur after initiation. So the initiation is the necessary and sufficient condition for breakdown.

      At present there are only few physical models considering the initiation of an electric discharge in liquid due to processes in bubbles [1-6]. The number of experimental dependencies of electrical strength gets non-contradictory explanation in models: volt-time features, dependencies on pressure, dependencies on viscosity, dependency on dielectric permeability, dependency on temperature, effect of electrode polarity, area effect. Moreover, particularities of these dependencies in different combinations of parameters are explained.

     But there are several problems in bubble models: the possibility of stationary existence of bubbles, mechanisms of bubbles emergence, mechanisms of charge carriers emergence, behavior of a charge in bubbles, ionization processes in bubbles, in particular the time for breakdown development, hydrodynamic phenomena, transition of the discharge into a liquid phase. Besides direct experiments, confirming or refusing proposed bubble model are absent. This is connected with experimental difficulties, as follows, with small sizes of active bubbles and very short time duration of the event. Required spatial scale is from 1 to 10 mm, time duration is from 10 ns to 1 ms. As for as the registration of space-temporary behavior of such objects it is very difficult task.

      The aims of this work are the search of experimental confirmation of bubbles’ role in breakdown initiation and development of bubble model. The first step should be the attempts to find the events that could be consequences of processes in bubbles. For instance to compare the places of breakdown initiation with the location of existing bubbles, to compare a possible field distortion with ionization in bubbles, etc.

      In our studies concerning the prebreakdown processes in nitrobenzene by means of electrooptical Kerr effect [7-9] were registered number of events, which points to the role of bubbles. Kerr effect performed to show both the electric field distribution and optical picture. The liquid had the conductivity that correspond to the Maxwell time of the dielectric relaxation approximately equals 30-40 ms. The electrode system “point-plane” with point radius of curvature 300 mm guaranteed the prebreakdown processes in small area. Voltage pulse was risen during 3-5 ms and fallen during 50-100 ms. Maximal electric field was 500-1000 kV/cm. There was two main regimes to take pictures: the line split streak of the light that passed from the laser through the central line of the gap and the multi-frame picture of the near electrode vicinity. In last case the exposure time was 50 ns and the time interval between frames was 5-7 ms. The cell was inserted between crossed polarizers in optical scheme.

      On the fig. 1 it is shown the picture of the split streak of prebreakdown processes at the influence of voltage pulse of negative polarity [7,8]. The regular fringes were due to the Kerr effect. Lines of equal intensity approximately correspond to the equal electric field strength. On the voltage rice the point of the same field intensity should move from electrode. Therefore the line of the distant fringe patterns repeats the form of voltage pulse. If the local field intensity is distorted the corresponding fringe changes it’s form. It can be seen on the fig. 1 where fringes close the electrode sufficiently bend. Electric field decreases close to electrode surface. It is caused by the emission of carriers of negative charge (homocharge). The point of fringes crooks moves from electrode. The estimation of the velocity gives 20-40 m/s in the field 0.5- 1 MV/cm. It equivalent charge carriers mobility (5± 2 ) 10^-3 cm² V^-1 s^-1 and well correspond to the electrohydrodynamical nature of conductivity at pulse voltage.

         Dark lines cross the Kerr fringes near electrode, but its trajectories don’t cross the line of charge front. Analyses of this fact and the data that will discuss in the next section shows that it is bubbles. The slope of the trajectories is practically the same as the slope of the charge front line. So practically the same velocities of charge carriers and non-charged bubbles is another confirmation of EHD flows development at microsecond voltage pulses.

        And, finally, on fig.1 one can see two jumps of Kerr fringes, which caused by the instant redistribution of local field. At moments of redistribution of field intensity the local area close to electrode is filled by microbubbles. Close to this area the Kerr fringes jump and electric field is sharply increased. The location of Kerr fringes far from bubble's area isn’t changes. That is why the electric field far from the bubble's area doesn’t change its level. The local increasing of the electric field intensity points out three ionizing events in the bubble area. Moreover last ionizing cause the breakdown of gap. The bubble model of breakdown initiation leads to the same conclusions: repeated process of ionization in bubble close to electrode and start of breakdown channel at some moment.

Fig.1. The picture of the split streak of prebreakdown processes at the action of voltage pulse of negative polarity in nitrobenzene. Jumps of Kerr fringes shows local ionization processes in bubble area.

      These bubbles are situated along the electric field line close to electrode [9]. According to the bubble model [4-6] the growing bubble at an elongation b/a> 3-4 can be unstable and one can be divided into two or more bubbles. It is the accidental process. Estimation shows that the instability of elongated bubble will develop preferable faster than breakdown initiation if field intensity is not sufficient for initiation during 10-20 ms. Past the process of dividing the events should repeat with the new bubbles that are situated close to electrode. New bubbles that are far from the electrode should move away from electrode. Therefore the chain of bubbles should be near electrode as a result of this process. Besides, the bursting off bubble should have a charge. It helps bubble to move, it supplies bulk by the space charge and it should support the electrohydrodynamical motion.

       The sequence of frames of near electrode area is shown on fig. 2. Field strength at maximum is 500-600 kV/cm approximately, voltage of negative polarity, no breakdown initiation. At the bottom of frame is electrode, quasi-parallel lines are Kerr fringes and dark dots are the bubbles. The first frame was at the moment of maximal voltage. Kerr fringes practically repeat the form of electrode. Electric field is slighting distorted at the left side of electrode.

      The second one was at the voltage decay 10 m s past voltage maximum. The electric field is decreased at the place where the bubble is situated. The most interesting fact, registered in this frame, is a chain of elongated bubbles situated along the line of electric field. One can see that the elongation of bubbles in the field direction not exceeds 3-4.

       The third frame was obtained at the 15 ms past the second one. At the moment of this frame the voltage at the gap is small in comparison with pulse amplitude value. It follows from the presence of wide Kerr fringe far from electrode. On the place of bubbles at previous frame here is situated several bubbles that are practically non-elongated.

       Formation of a chain of bubbles, on our point of view, one can be simply explained in terms of bubble model. Optical and electrooptical data (elongation, field distortion, and the chain of bubbles) well correspond to the consequences of the bubble model.

Fig.2. The sequence of frames of near electrode area at the low voltages in nitrobenzene. One can see elongated bubbles on second frame and the chain of bubbles on the third frame.

       According to the model the size of most dangerous bubbles is 2- 20 m m at the action of electric field from 100 kV/cm to 1 MV/cm. More probable that the big bubbles can break out by the another mechanism, f.e. due to criteria “avalanche - streamer” transition. Nevertheless it is very important to register the events that are in this case. The sequence of frames with preexisted bubble is shown on fig.3. The bubble which size is near 50 m m is based in area of center, a little distance from the central electric field line. The next frame was at the moment of maximal voltage. Analyze of Kerr fringes gives a lot of information about tree propagation. The presence of Kerr fringe near electrode shows that certain electrical field stays in this area (~30% of the field that should be without tree). So the potential is not followed the tree branches. The preexisting bubble transforms into shapeless body. The fringe at the right side of this region points out to the space charge inside. One can see two branches originate here. The left branch is stopped, Kerr fringes near it’s front very sharp. Field intensity at the top of this branch is insufficient for tree propagation. The right branch is the fast moving object. The far wide Kerr fringe shifts away from electrode. That is why the electric field in front of branch is high enough. Moreover, field is sharply intensified in the vicinity of branch tip. It can be seen in fig. 3 from the fact that the Kerr fringes are absent here. The reason of this behavior is next. During the time of exposure the phase shift of transmitted light become indefinite due to moving of the tip and the change of the field. In this case, at the beginning of exposure (50 ns) the light has one phase shift, so the transmitted light has a definite intensity. At the another moments of the exposure the light has another phase shift and transmitted one - another intensity. The average intensity is half of the maximum approximately and on the sharp black-white photo it leads to disappearing of the fringes.

The last frame shows a breakdown that originates on the site of the preexisted bubble.

Fig.3. Breakdown initiation due to pre-existed bubble in nitrobenzene. First frame – before voltage action, second frame – at maximal voltage, third frame – development of breakdown area.

      In these experiments, performed by Ponomarenko A.G. and Klimkin V.F. [10] was used multi-frame Shlieren system with the high space resolution (not worse 5 mm) and short exposure (5 ns). Interelectrode gap was 2 mm, radius of hemispherical electrodes 25 mm, field intensity 600 kV/cm, flash of exposure - approximately 50-60 ns after the completion of front of pulse, electrode - an anode. According to our opinion [11] on fig.4 one possible to see several microbubbles on the surface of the electrode. Their sizes are 20-30 mm. Before the electrical stress the bubbles were absent here. Therefore the velocity of their grows is more than 10⁴ cm/s. One should undoubtedly note that it is bubbles, because bubble image should be dark with light spot in the center of the bubble. Such kind of object is on fig.4. Herewith one can clearly see the deformation of single bubble in direction of the action of electrical field. On fig.4 pointer directs on this bubble. If pay much attention on this bubble it is possible discover that near the poles of the bubble is registered the cone edge with indistinct image of branching formation. The image of the cone is sharp enough but branches image is more diffuse. The size of area, including branches, is not less than 100 mm.

       The most plausible explanation of these facts consists of following. Bubble grows at the action of strong electric field and one is deformed as predicted by prebreakdown process model. Its lateral borders sufficiently sharp so the bubble doesn’t grow in diametrical directions.

       Transverse size of bubble is approximately 20 mm, longitudinal size is not less than 40-50 mm. It is imagined that this frame is sufficiently unique. It seems that initiating streamer has occurred at a moment close to the middle of exposure duration. In this case it is explained both more optically thick base of cone and more spreaded branches of growing tree channel.

Fig.4. Several microbubbles on the fragment of the electrode surface in n-hexane at the electric field stress. Arrow shows most elongated bubble from which breakdown channel initiates at the exposure.

      A problem of a mechanism of bubble existence is fundamentally important for the studies of the processes of boiling and cavitation in liquids. Gas bubbles must leave the bubble being dissolved in liquid as it is subjected to additional pressure due to capillary forces. Time of dissolving t _s depends on size r,

               (1)

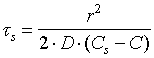
      It is seen, that the bubble may have kinetic stability either liquids where diffusion coefficient D is small (large viscosity) or at small gas solubility Cs or at dissolved gas concentration C closed to limiting gas content Cs.

      There are several models of static stability of the bubble. Surface of bubble can absorb surface - active substances, which form a hard film on the surface. The film maintains the size of the bubble and the gas pressure is the same as in the case of the flat surface.

      A more probable variant for gas existence is associated with the presence of an electrode surface relief, namely: pores and edges as well as clustered microparticles. In this case there is a set of pores in which the stable bubbles can exist.

     The optical experiments of the bubbles behavior in water have shown that in the distilled, filtered out water there permanently exist 10³-10⁴ l/cm³ bubbles of micron sizes [12]. To explain this effect it was suggested a mechanism of interaction of gas with liquid in view of physical adsorption of gas molecules on the surface. In this case, on the authors’ opinion [12], there may be equilibrium of the dissolved gas both with gas over the flat surface and with gas inside the bubble.

     Nevertheless, at careful preparation of the liquid and the cell one managed to reach overheating P- P_s. relative to equilibrium temperature T_s when P (T)>>P (T_s) or to reach tension when outer pressure is negative P_out<0. This meant that in the liquid there could be the very small nuclei only of submicron sizes.

     Resuming the results of the studies one can declare that under ordinary conditions of the experiments the microbubbles of micron sizes are present in liquid, especially on the electrode surface. For very pure conditions and at small area of the electrodes only the nuclei of submicron sizes are expected to be present.

     Earlier [13] it has been shown that the influence of the electric field of strength E upon the bubble is equivalent to additional pressure

       (2)

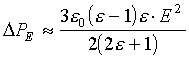
where e is the dielectric permeability of liquid. In principle to form a bubble it is necessary to realize the ordinary mechanisms, namely: overheating or cavitation with additional pressure (2) being taken into account.

Overheating. For the case of pulse action the electrical conduction of liquid dielectrics is sufficient to create overheating for the electrolytes only.

      The relief of the electrode surface causes the field amplification and the increase of the current density near the microedges. According to [14] the typical values of the coefficients of field amplification close to the microedges of a roughly treated surface may be 200. In the case of the ohmic behavior of an “electrode - liquid” system the local specific energy release in the field of mean strength 100 kV/cm during 1 m s will be more than 1 kJ/cm³ at electrical conduction more than conductivity of distilled water 10^-6 Om^-1 cm^-1

      To estimate the energy release in the case of nonlinear behavior let us invoke the data on studies of conductivity in a “point-plane” electrode system. Numerous experiments [see f.e. 15, 16] have shown that the dependence of current upon voltage I (U) has 3 characteristic stages: linear dependence at small field, sharp growth in 2-3 orders of magnitude while reaching some strength and then the transition to weak dependence I ~ U². The first stage corresponds to the Ohm’ law, the second one - the field emission of the charge carriers from the electrode, the third one - space charge limited current (SCLC). The estimations of strength of the transition to SCLC mode show that in non-polar liquids of hexane type this occurs at comparatively low local strength E_e~10⁷ V/cm. A weak dependence of local strength upon the voltage is a characteristic feature of the SCLC mode. To estimate the energy release W let us consider that the field at electrode doesn’t depend upon the voltage and is equal to E_e.
       For instance, the conditions for non-polar liquid with e =2 are: microedge top radius is 10^-5 cm, the field amplification coefficient is 200, local strength is 2 10⁷ V/cm, average field strength is 100 kV/cm, pulse duration is t=100 ns, the current mode is close to the SCLC mode, mobility of charge carriers is m ~10^-4 cm²/(V s). One can show that at the beginning of the transition to the mode the charge density will be equal to:

The release energy density W is high enough for a homogeneous nucleation with extra pressure D P_E (2). As a result of this process there may be the formation of bubbles of submicron sizes.

Cavitation. In the electric field Coulomb force of density  f=r _SC  E   affects the space charge r _SC. At the hydrostatic equilibrium this force is balanced by a pressure gradient in liquid. In this manner a tension area may appear. At emission of carriers from a plane electrode the pressure near it decreases in relation to external pressure P_out

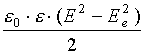                      (5)       

Here E_e is the field near the electrode decreased due to emission. From (5) it is seen that the cavitation under the stress of strong electric fields is possible only at decrease of a field near the electrode (electrode screening). Strong screening is supposed in polar liquids only. There exist so-called double electrical layers consisting of ions partially located both immediately on the electrode surface and partially distributed close to them. One is supposed that double layer may serve as an ion injector from a cathode usually. If E_e is sufficiently small in comparison with E, then the pressure becomes negative at: 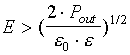                                                                                                                                                                               (6)

The estimations show, f. e., for water that the pressure will become negative in the field with strength E  150 kV/cm. But in this case only the heterogeneous nucleation from pre-existing microbubbles may take place.

The negative pressure of order of 1000 atm is required for the homogeneous nucleation. This can be realized in microscopic region only. For the field of the microedge it is impossible to obtain a simple formula like (5) type. The only case when one can solve this problem analytically is the established mode of SCLC. For micropoints of radius 10^-5 cm the mode can be considered as established one at pulse duration more than 10 ns. It is clear that for the conditions of electric breakdown this requirement is satisfied. One can show that the pressure near the point may be estimated by:

            (7)                                                                                                                                                                                               

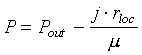
Here j is the current density. Numerical estimation for conditions (3) give negative pressure of P~ 400 atm.

Hence the bubbles may appear close to electrodes due to the tension in the “macro” area of the space charge. In microareas of field amplification the bubbles may appear both due to the cavitation and due to boiling at the high level of emission field.

At pulse stresses the primary electron appearance is important because it defines a moment of discharge initiation. The studies of gas discharges have shown that one should take into account such mechanism of generation of charge carriers as: the emission of electrons from a cathode by positive ions, decay of negative ions due to temperature and electric field action. The most probable origin of electrons is decay of negative ions such as H₂O^- and O₂^- which electron affinities is j ~0.9 eV. A value of the time of ion decay t , may be estimated by the expression

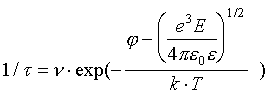              (8)

 Assuming the vibration frequency to be n ~10¹⁴ 1/s and taking into account the fact that for E=1 MV/cm a “Shotttky” decreasing of the barrier equals to 0.38 eV, one will obtain t » 10^-5 s. It is clear that according to this mechanism the initiation of pulse breakdown possible in the case if there is the number of negative ions in the initiating bubble. The other mechanism may be associated with the collision of the negative ion with the neutral molecule, f.e.,

O^- +N₂ « N₂O + e.                    (9)

The constant of that kind of reactions have an order of magnitude 10^-10-10^-12 cm³/s [14]. This means that at the atmospheric pressure an electron release will occur in nanosecond times.

A problem of primary ions couldn’t be solved without the electrode. The presence of ions in a gas phase of the bubble is doubtful. The ion can reach the bubble either from the bulk of liquid or from electrode surface. If the charge distribution near bubble is identical with that one in the bulk of liquid it can be shown from the value of conductivity that for liquid dielectric with bubble size of 1 m m there is about 1 ion close to it.

In the case of the liquid with great electrical conduction, water, the number of ions is considerably greater and may be more than a thousand close to one bubble. This raises the question of whether the concentration of ions near the bubble increases or decreases as compared with the bulk concentration.

It is well known [17] that near the boundary of the phase with permittivities e ₁ and e ₂ “image force” affects to charge:

                (10)                                                                                                                                        

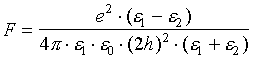
      Here h is the distance from the charge to the boundary. The positive sign of force in case of bubble surface denotes that the charge repels from the boundary. This means that near bound ion deficient layer must exists. One can estimate that a size of this layer in non-polar liquid with e =2 yield h~2 nm and in polar liquid with e =80 (water) h=0.2 nm. The value of the field strength at the boundary of this area, as the ion approaches to the surface, will be 100 kV/cm in the case of the non-polar liquid and 1 MV/cm in the case of the polar liquid. It is of interest that if the ion approaches the boundary from the gas phase side, then the image force changes its sign.

     What role can the considered effects play at the ionization processes in bubbles? Firstly, the charge carriers are to adhere to the walls of the bubble and, secondly, are to be expelled by the bubble surface inside the bulk of liquid.

      A similar effect is to appear at “metal-liquid” boundary. For a metal one may formally take e as infinity. After that (14) is presented in the form:

                (11)

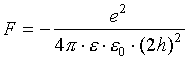
     It is seen that the force is negative that corresponds to the attraction of charges from the dielectric liquid to the surface of the metal making the layer with the increased ion concentration.

     The image forces cause one more new mechanism of the formation of double electric layers and surface conductivity near metal electrodes and surfaces of the samples with high permittivity. Ionization and dissociation are promoted in dielectric liquids as compared with gases due to greater dielectric permeability as the ionization energy is reduced in e times [18]. The presence of an adjacent phase with high dielectric permittivity facilitates the dissociation of molecules. Let dissociation occurs in the close-to-surface layer and the formed divided charges not leave the surface. Considering “image” forces acting on charges one can obtain that it should decrease the attractive force between divided charges. Estimations gives the ionization energy decreasing and for this case it is approximately W_is=2/3 W_iv. This means that near the surface the ionization occurs considerably easier and, consequently, there the charge carriers concentration is larger and the surface electric conduction is higher. This fact gives rise to additional mechanism for the formation of the electric double layer and provides an explanation for the presence of the high conduction surface layer.

     The characteristic of the field in which these processes take place is 100 kV/cm-1 MV/cm. The pressure in the air filled bubble may be considered to be 1-10 atm. For this case E/p is 100-1000 V/(cm  Torr). It is known [14] that for the range E/p» 100-800 V/(cm  Torr) ionization coefficient a is well approximated as:

a ¤ p= A exp(-B/(E /p))                       (12)

where A=15 (cm Torr)^-1, B=365 V (cm Torr). The estimations from (12) show that a is to be approximately equal from 700 l/cm up to 8000 l/cm. For bubbles of 1-10 m m sizes a  d» 2-3 that is considerably less than 18 that is needed for an avalanche - streamer transition. Thus, the breakdown in the microbubble is to occur according to the Townsend avalanche mechanism. As a result of passing of one avalanche more than one “effective” electron is being generated at voltage across the bubble higher than the one according the Pashen curve. The coefficient of the avalanche multiplication is in form:

b = g  (ea ^d-1) >1                     (13)

where g is the secondary coefficient of impact ionization causing the appearance of the secondary avalanches in the bubble due to photons or positive ions. By definition equality in (13) defines the Pashen curve U=f(p d) or in another form E/p=f (p d).

           Hence one can estimate the time of the bubble breakdown as it is connected with both coefficient b and the time of ion drift in the bubble gap t _i =d/(m E (b -1)) [18]. The prebreakdown time is equal to infinify   at the Pashen curve. One should to estimate b for the bubble at the voltage above the Pashen curve. Here one can use the standard procedure to calculate b close to 1 at the rise of the field from value E₀ at the Pashen curve up to value E.

,

Then by using (12,13) one can obtain:

        (14)

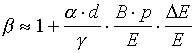
        Substituting the value of the parameters at the equilibrium line one get, for field strength 100 kV/cm, b -1» 13 D E/E. It means that at the growth of field of 10% above the Pashen curve the time of breakdown of the 20 m m size bubble will be negligible in comparison with usual pulse duration. Assuming mobility m ~1 cm²/(V s) and neglecting the field amplification in the bubble, one get that the breakdown time will be 2 ns. So one may neglect the time of the formation of the microbubbles breakdown.

         One should point out that after the discharge in the bubble, from the side turned to the anode, the electrons are inserted into liquid and from the opposite side the positive ions interact with the surface. It is apparent that interaction of electrons and ions with liquid molecules is differed. It is probable that the electrons are to penetrate more deep into the liquid and after the thermalization they move in accordance with their mobilities. That’s why discharges in the bubbles are to cause different consequence for the anode and cathode located bubble.

        Neglecting the change of pressure due to temperature let us estimate the Coulomb force affecting the charged wall with surface charge s _s in direction of field after the discharge in it.

.             (15)

       Discharge can be periodically initiated or stationary supported due to the motion of charges being appeared on the walls and then in the liquid.

In expression (16) value r is of great importance. From the point of view of electric breakdown the bubble with a size given below will be the most dangerous:

r_c = U_p(2e +1)/6e E                              (17)

where U_p – Pashen’s voltage of bubble breakdown. So in expression (16) one substitute unknown r for defined r_c and obtain an expression for the average pressure on the bubble wall [20]:

               (18)

In the case of a quasi-stationary discharge in the bubble, for the case of the adherent charge namely, equivalent pressure is:

                 (19)

where K is the coefficient of field amplification.

       In the calculations of the bubble dynamics let us ignore the fact that the bubble increase in field direction only and assume that average pressure P_pd affects the wall. The equation of the bubble wall motion can be written by analogy with the well-known equation of motion of the bubble wall under the influence of pressure difference:

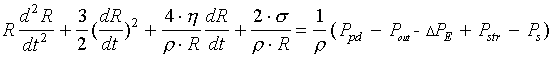
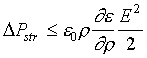
        Here h , s is the viscosity and surface tension coefficient of liquid, P_s is vapor saturation pressure. Equation (20) is the basic equation of the model and it allows us to compute the bubble growth with discharge acting in it and obtain the dependence of time of growth upon the external factors and properties of liquid for different kinds of bubbles in liquid and on the electrodes. In a one case one may obtain an analytical solution [20] that describes the evolution of bubble with the hard film of surface - active molecules at the action of rectangular voltage pulses.

       As the bubble elongates in the direction of the electric field there can be several new processes concerning the transition to liquid breakdown. The first one is the transition of discharge from Townsend type into streamer one. Estimations show it is probable for big spherical bubbles preexisted on electrodes. The second one consists of electric field increase in the liquid near poles of elongated bubble. It should be past the discharge in. The increase is very important factor, f.e. if bubble can be treated as ellipsoid on surface, the coefficient K reach 20 approximately if it’s elongation reach 3. For elongated bubble in form of cylinder with hemispherical top the coefficient K is less. However field can be of such size, that was rather for electronic multiplication in a fluid. For some field strength near electrodes there is some elongation at that field near poles reach some critical value E_m. If propose that cross-section of bubble is not change, the discharge can start in liquid at the some elongation. In computations E_m will be single parameter.

        As one was mentioned above, if discharge initiates it can’t be stopped if electrode system forms uniform or slight non-uniform field. So the full prebreakdown time can be divided into three parts t=t₁+ t₂ +t₃, where t₁ - time of bubble emergence, t₂ - time of bubble deformation up to breakdown initiation, t₃ - time of breakdown tree propagation from one electrode to the another one. For small interelectrode gaps that usually applied in breakdown experiments values t₁ and t3 are small t₁<<t₂, t₃<<t₂. Hence one can identify time of bubble deformation with the prebreakdown time.

        Some basic factors that define electrical strength in model are the pressure, pulse duration, dielectric permittivity, viscosity. The volt-time characteristics, pressure influence, electrode surface area effect can be treated from (20) [6, 20, 21]. Comparison of computed and empirical data performed to obtain the rough estimation of critical value E_m for the most liquid Em » 10 MV/cm. Computed curves for n-hexane, ethanol, glycerol, water well correspond the empirical Martin’s expression. For example fig.5 shows conformity of computed and empirical data for water. Numerical coincidence is chance because of the absence of the electrode area information in model. As for as pressure dependence there are several peculiarities. The time to breakdown at permanent fields is practically proportional to pressure. The less pulse width the less pressure dependence [11].

          Research and educational computer program “Bubbreak” (see Appendix) is based on bubble model of breakdown initiation. The physical basement performs to compute and to show the most of breakdown dependencies

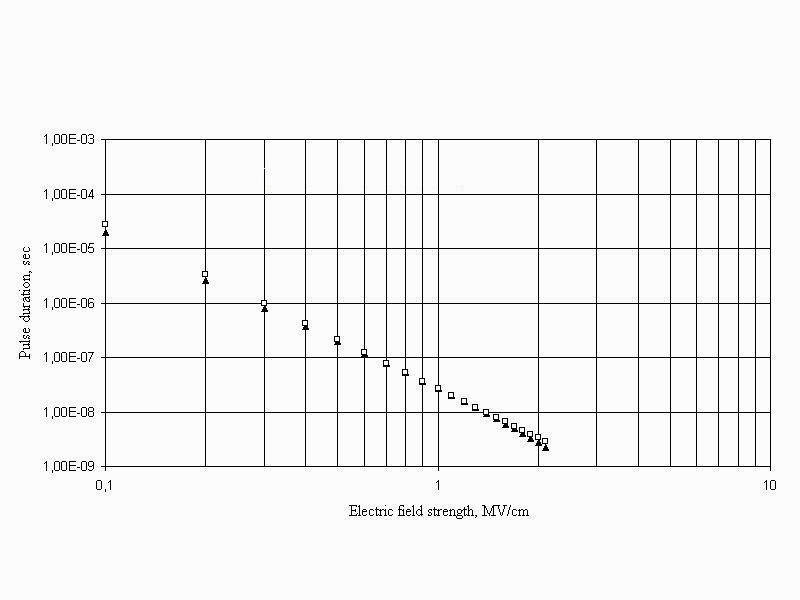
Fig.5. Computed and empirical time-volt dependencies. Rectangular marks show well-known Martin’s expression, triangular marks show our computations.

     Optical and electrooptical experimental data on prebreakdown processes both in polar liquid (nitrobenzene) and non-polar liquid (n-hexane) show that bubbles play the important role in breakdown initiation. It isn’t direct confirmation of the bubble model but these facts not contradict the theoretical model. Most bright facts are repeated ionization in bubble area, the chain of bubbles near electrode, coincidence of the site of preexisted bubble with the place of breakdown emergence, the tree origin from most elongated bubble in n-hexane. On the base of bubble models of breakdown initiation in liquids is offered non-contradictionary explanation of main experimental dependencies of electrical strength.

      Proposed model explains from unified positions dependencies of electrical strength and prebreakdown time duration on external factors, characteristics of liquid and properties of bound “electrode - liquid”, geometrical parameters of electrode system and pulse width of voltage.

      Computer program “Bubbreak” is based on bubble model of breakdown initiation. The physical basement performs to compute and to show the most of breakdown dependencies.

RFBR (grant 98-02-17903) and Ministry of Education (grant 97-5.3-114) supported this work.

[1] H. M. Jones and E. E. Kunhardt, “Development of Pulsed Dielectric Breakdown in Liquids”, J. Phys.D: Appl.Phys. 1995, V.28, P.178.

[2] O. A. Sinkevich and P. V. Smirnov, “Heterogeneous Mechanism of Electrical Breakdown of Liquid Dielectrics”, J. Moscow Phys. Soc., 1996, V.6, P.101.

[3] I. Alexeff, M. O. Pace, T. V. Blalock, A. L. Winterberg, “Possible Models for the Earliest Prebreakdown Events in D.C. Stressed Hexane”, Conf. Record of the 10-th Int. Conf. on Conduction and Breakdown in Dielectric Liquids, 1990, Grenoble, France, p.387-391.

[4] S. M. Korobeynikov, E. V. Yanshin, I. T. Ovchinnikov, K. V. Yanshin, S. G. Sarin, V. M. Kopylov, A. V. Klepikov, “Physical Processes Limiting the Pulse Energy Release in Liquid Dielectrics”, Technical Digest of the Int. Conf. on Pulse Power, Albuquerque, 1995, p.574-579.

[5] S. M. Korobeynikov, “The Role of Bubbles in the Electric Breakdown of Liquids: Prebreakdown processes”, High Temperature, 1998, Vol. 36, No. 3, pp. 362–367.

[7] S. M. Korobeynikov, E. V. Yanshin, K. V. Yanshin, “Prebreakdown Processes in Liquid Insulation at Pulse Voltage Action.// In book: “Impulsnyi proboi v dielektrikakh”. Ed. acad. G.A.Mesyats, “Nauka Publ.”, Sib.branch. 15 p., 1985 (in Russian)

[8] S. M. Korobeynikov, E. V. Yanshin, K. V. Yanshin, “Space Charge and Prebreakdown Bubble Formation near Point Electrodes under Pulse Voltage”, Conf. Record of the 8-th Int. Conf. on Conduction and Breakdown in Dielectric Liquids, 1984, Pavia, Italy, 5 p.

[9] K. V. Yanshin, “Optical Studies of Prebreakdown Processes in Polar Liquids at the Action of Microsecond Voltage Pulses”, Ph.D. Theses, 1983, SibNIIE, Novosibirsk (in Russian)

[10] V. F. Klimkin, “Optical Studies of Pulse Breakdown of Liquids”, Ph.D. Theses, 1977, NGU. Novosibirsk (in Russian)

[11] S. M Korobeynikov, E. V. Yanshin, K. V. Yanshin, “Experimental Evidence of Bubble Model of Discharge Initiation”, Proc. Int. Conf. on El. Insul. and Diel. Phen. 1998, p 436-439.

[12] A. C. Besov, V. K. Kedrinskii, E. I. Pal’chikov, Y. Matsumoto, F. Takemura, H. Ohashi, “Threshold Cavitation Inception by Pulse Rarefaction Wave”, Proceedings of the 68-th Conference of JSME, v.B, Sendai, 1990.

[13] S. M. Korobeynikov, “Vliyanie Electricheskogo Polya na Tochku Kipeniya Ghidkostei”, Inghenerno-Phizicheskii Ghurnal, 1981, N 6, P.1131 (in Russian).

[14] Iu. D. Korolev, G. A. Mesyats, “Physics of Pulse Breakdown in Gases”, Moscow: Nauka publ. ,1991. (in Russian)

[15] W. F Smidt, W. Schnabel “Electron Injection into Dielectric Liquids by Field Emission”, Z. Naturforth., 1971, V.26a, P.169.

[16] K. Dotoku, H. Yamada, S. Sakamoto, S. Noda, H. Yoshida, “Field Emission into Nonpolar Organic Liquids”, J. Chem. Phys., 1978, V.69, P.1121-1126.

[17] L. D. Landau, E. M. Lifshits, “Electrodynamics of Continuous Media”, Moscow, Nauka publ., 1992 (in Russian).

[18] Iu. P. Raizer, “Physics of Gas Discharge”, Moscow: Nauka publ., 1987, (in Russian).

[19] N. Felici, “Electrostatics and hydrodynamics”, J. of Electrostatics, 1977-1978, V.4, p.119.

[21] S. M. Korobeynikov, Yu. N. Sinikh, “Bubbles and Breakdown of Liquid Dielectrics”, Conference Record of the 1998 IEEE International Symposium on Electrical Insulation. Arlington, Virginia, USA, pp. 603-606.

Appendix A

Structure of the program.

Program consists of the following blocks:

a) Computation of prebreakdown time in case of discharge initiation at the anode or at the cathode. It depends on pressure, intensity of a field, temperature, size bubble - t(E, P, T, r₀). This is performed by the numerical decision of the ordinary differential equation of the second order.

c) Construction of the diagrams in logarithmic or linear scale;

d) Data input (choice of a liquid from library, change of parameters of computation and display), choice of required dependence, and also input of properties of a new liquid;

e) Information on the breakdown theory, instruction on work with the program and authors’ information;

f) Work with the user (student, or researcher) supposing registration, save, viewing and removal of the initial and received data.

Choice of dependence, which illustration you want to receive, is carried out by selection submenu “Parameters” which are taking place in the menu “Configuration” (fig.6).

For every chosen dependency the other parameters are assumed “constant” parameters. By default are established:

· pressure P = 1 atm;

· electrical field intensity E = 1 MV/cm;

· duration of a pulse width t = 1 ms;

· temperature T = 20° C;

· factor describing the relation of radius of investigated bubble to radius of “most dangerous” bubble, = 1.

       If select “Electrodes” it is possible to choose the form of an electrode, from which occurs breakdown (plane, edge, sphere), polarity of an initiating electrode (anode or cathode) and critical field intensity E_m. The data for n-hexane, glycerol, water and transformer oil are in library (by default is established n-hexane). If it is necessary to add in library of liquids one more dielectric liquid, the submenu of “Liquids” is necessary to select “New”. Dialogue window “Creation of a new liquid” requires input its parameters (name, dielectric permittivity, density and viscosity for temperature 20 ° C). For computation of temperature dependence it is necessary to set Ps (T) and h (T) by pressing on the button “ Temperature dependence”.

       For an illustration of model of discharge initiation in liquids the demonstration of prebreakdown processes was specially developed. At a choice of “Demo” in menu “File” on the screen there is a window of demonstration, in which it is possible to see model of interelectrode gap and bubbles that located on the electrodes surface. There are bubbles of three colors. It is “most dangerous” bubble of yellow color and two bubbles of red and white color, which sizes accordingly are more and less size than “most dangerous” bubble. One can see that process of breakdown initiation occurs as follows. After voltage action the growth of bubbles begins. Thus bubbles, having radius it is less than “most dangerous”, do not grow in general, since in them do not occur processes of impact ionization. As soon as “most dangerous” bubble will reach the size, sufficient for the initiation of breakdown in the liquid phase, modeling process of growth of breakdown tree begins. It is based on the model of the “cell automatic device”. In process of breakdown tree growth bubbles of red color continue to grow, though do not reach the deformation that is necessary for the beginning of discharge initiation from them. The breakdown occurs when one branch of tree touches the opposite electrode. The test of breakdown can be repeated by pressing on a key “Blank”, thus the initial (but another) arrangement of bubbles will be placed on electrodes surfaces. Pressing a key «Esc» carries out the exit from the «Demo».

The exit from the program is carried out by usual way.

The examples of computation of breakdown dependencies are presented in [2,3].

Fig.6. Choice of computed dependence in Windows version of computer program “Bubbreak”.