Abstract - The behavior of artificial bubbles of sizes 20-60 mkm in water is experimentally studied at the field close to 300 kV/cm. It was shown that bubbles are elongated in the direction of electric field, divided and moved from electrode. Comparison with bubble model shows that it's elongation don't contradict the model.

1 Introduction

The clearing of the reason of pulse electric breakdown of liquids is key problem of pulse capacitance devices. The current that could be supplied is determined by a density of an accumulated energy in a dielectric proportional permittivity of a medium and squared strength of a field. To the present time the greatest power is reached in case of usage of liquids with a high permittivity, in main deionized water. As the permittivity of liquids is the physical parameter and it cannot be increased, the problem of high currents is the problem of electrical strength increasing

The researchers usually deal with the stage of discharge development, i.e. they research the shape of streamers tree, it's charge, velocity etc. It concerns both experiments, and construction of theoretical models [1,2]. However in studies the key part of the breakdown process - initiation of discharge is poorly affected. The matter that an electrical breakdown in homogeneous, or slightly inhomogeneous electrical field, happens to all inevitability after its initiation, i.e. the initiation of discharge is necessary and sufficient condition of a breakdown. Therefore study of discharge initiation is in essence important for physics of a breakdown of fluids.

Bubble model of breakdown initiation allows to explain qualitatively (and in some cases quantitatively) the main dependencies of the electric strength on the pulse duration, pressure, temperature and so on obtained experimentally. It is presumed here, that micro-bubbles initially exist on the surface of electrode, the breakdown is initiated from them, and the impact ionization in liquid could take place only under the action of high electric field greater than 10 MV/cm.

Nevertheless the experimental confirmation of the model is absent. The aim of this paper is the study of artificial bubbles at the action of strong electric field.

2 Experimental

Experimental setup consists of: HV system with pulse voltage generator up to 100 kV with pulse rise 200 ns and pulse decay 50 ms; optical system of bubble visualization and photo registration with

light pulse duration t~30 ns; system of bubbles generation on the surface of electrodes; the system of synchronization (Fig1).

Fig.1. Experimental setup.

1- test cell, 2- current supply, 3- relay,

4- stationary laser, 5- microscope,

6- HV power supply, 7- ruby laser OGM-40,

8-synchronize device, 9- photodiod,

10- oscillograph S8 – 14Bubble generation

The generation of microbubbles is carried out by pulse heating of quasi-needle electrode representing U-formed loop from nichrome wire by a diameter 0.2 mm, with radius of a bend of 0.5 mm. The wire is put to earth after the pulse of a current, opposite high-voltage electrode is a plane. Duration of pulses of a current by amplitude up to 3 A varies with the help of the relay of time in a range 0.1-5 s.

Bubbles are not in equilibrium in liquid and dissolve during some time duration t_s. This time is proportional to squared radius r² and depends on the level of air content C (cm³/ cm³). Analyze shows that these data don't contradict model of dissolving of air bubble

(1)

where D - diffusion coefficient, C_s- air content at saturation. This confirms by experiments in tap water, where bubble of 50 mm radius disappears during 6 min., while in slightly saturated water the same one disappears during several seconds.

Computations of the threshold of bubble appearance are performed. Experimentally and by computing it is shown, that 100-200 mm bubbles are appeared at the surface when the temperature near wire surface is more than boiling temperature. For example threshold in distilled water that are in equilibrium with air is 0.4 s at the current 1.8 A (Fig. 2.). Past appearance the size of bubble decreases very sharply during one second.

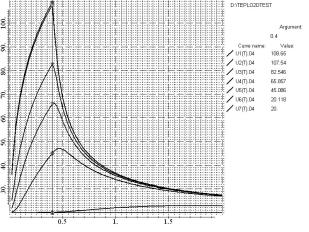
Fig,2. Dependencies of temperature on time at different points:
U1- at center of wire, U2- at the surface, U3, U4, U5, U6, U7- at distance 50 mm, 100 mm, 200 mm, 1 mm, 2 mm from wire.

After that at the surface of the quasi-needle there is long-lived slightly decreased microbubble by the size 10-100 microns. This bubble is ready for prebreakdown experiments. One should note that in degassed water there no bubbles at current up to 3 A and time duration up to 10 s.

After an establishment of temperature balance near to wire (~ 1 s), or after some period of time delay that necessary for reduction of the sizes too large bubble, to electrode system «quasi-needle - plane» applies a voltage pulse. In this experiments the quasi-needle electrode has "earth" potential, opposite electrode has positive or negative polarity. The intensity of an electrical field near to wire is necessary specially to compute, since for used electrode system there are no analytical decisions. On fig.3 it is shown the lines of equal field intensity in the plane of wire bend. One can see that field at the tip very slightly depends on distance along surface. Field computation at the perpendicular plane leads to the same conclusion. As for as space distribution in vicinity of wire it can be estimate as cylindrical one.

Fig.3. Electric field near bent wire electrode. Figures show field intensity (kV/cm) at voltage amplitude 100 kV.

2.a Bubbles recording

The method of bubble behavior study consists of receiving of two pictures of bubbles on wire electrode: the first one before voltage action and the second one at the fixed moment during voltage exposure. Some results at the action of electric field on preexisted bubbles are shown on fig.4,5. Here the electric field intensity close to top of electrode is 300 kV/cm, moment of exposure is 4 ms past voltage rise. Polarity of wire electrode is negative. Several formed bubbles of 35-60 mm are on electrode surface. Due to curvature of electrode in direction of laser beam one can see full size of bubble only for those bubbles that are close to "visible" contour of electrode. From this picture and another pictures at different moments and field intensities one can see that bubbles:

- elongate in the direction of electric field;

- decrease in perpendicular direction;

- can divide on several bubbles (past 5-10 ms);

- the less bubble size – the more deformation;

- at the early stages bubble’s surface have some small scaled disturbances;

- the motion of bubbles at the times about 30-50 ms have electrohydrodynamical nature.

The main peculiarities of cathode bubbles are presented at pictures concerning anode bubbles. One should mention several differences. The first one is that сome off bubble has spherical form and stayed part of bubble looks like spread disk or cone on the surface of electrode. These facts are shown on fig. 6, 7. Bubbles number 1,2,3 that are situated close to the visible contour of electrode left flat rest on electrode past removing of the come off bubbles.

Fig.4. Bubbles configuration on cathode before the action of electric field.

Fig. 5. Bubbles configuration on cathode, 4 ms of the action of electric field E_max=300 kV/cm.

Fig.6. Bubbles configuration on anode before the action of electric field.

Fig.7. Bubbles configuration on anode, 8 ms of exposure of electric field E_max=200 kV/cm.

3 Theoretical and discussion

Let's analyse the contribution of various forces to movement and deformation of bubbles. What forces should act on them in a motionless liquid? Firstly, it is usual force that effect on bubble walls from electric field and leads to small elongation of bubble in the direction of electric field and more marked compression of bubble in diametrical directions. The deformation is proportional to radius and squared field intensity [1]

(2)

Here s is surface tension coefficient. Relative decreasing of volume due to this factor is [2]

(3)

Secondly it is known force caused by a difference of dielectric permittivities of liquid and gas bubble that appears in case of inhomogeneity of electric field, so-called dielectrophoretic force [3].

(4)

where D - dipole moment of bubble, which for spherical bubble of radius r is

(5)

For axial case F_d is approximately

(6)

where R - distance from the center line of wire.

The third factor is partial discharges in bubbles. Bubbles elongation in this case one can compute with the help of bubble model of breakdown initiation [4,5]. Emergence of surface and space charge near bubble's poles due to discharges leads to bubbles deformation due to Coulomb forces. Equivalent pressure in the direction of electric field is

P = 3e₀eE ²(mEt/r + 1 )/2 (7)

where m is mobility of space charge in liquid, t - time duration of electric stress.

The fourth factor is more disputable. It can be in work if uncharged bubble is in a zone of a space charge and the volume of this zone are in mechanical equilibrium. So in this region Coulombic force is balanced by tension in liquid. In this case the force that act on uncharged bubble push out it in the direction, opposite to movement of charge carriers. On the first sight, the origin of this force is difficult for understanding, however actually action of this force on bubble can be imagined similarly to action of usual buoyancy force on bubble in water. Both in that and in the other case the force works on a liquid and it is equivalent to action of the opposite directed force on bubble. Therefore the expression for the force on bubble F_sc in region of space charge by density

F_sc = - r_sc×E× V_b (8)

r_sc is where V_b is volume of bubble. In case of space homocharge near electrode the force F_sc will move bubble to electrode surface. In another case it will push bubble out of electrode area.

The last factor that should be considered is instability of bubbles. There are instability of two kinds. The first one is usual instability of bubbles due to oscillation. The action of field and Coulomb force should generate the mode of oscillation concerning elongation and dividing of bubble into two or several bubbles. Without electric field lower frequency of bubble oscillation correspond
(9)
All above mention factors should increase the frequency of bubble oscillation. Another variant is low scaled disturbances due to instability of charged surface at the action of electric field.

Fig. 8. Comparison of computed (curve 1,2) and

experimentally measured (marks) elongation of bubble 55 mm

in electric field 100 kV/cm.

The wavelength of instability is [6]:

(10)

Here s_s is surface density of charge. In case of fully charged bubble surface (and fully discharges bubble), as assumed in bubble model [4,5]

(11)

Substituting one can get

(12)

3.a Discussion

Comparison of the factors shows the next. Voltage across the bubbles of diameter 30-60 mm will be enough for discharge in bubble at the field intensity more than 100 kV/cm. Therefore discharges should be practically in all of registered bubbles. Coulomb force should be at least factor e (e=80) much more than the force that elongates uncharged bubble. Besides, deformation according (1) is proportional to r, so will lead to higher deformation of large bubbles. It contradicts to experimental data. The dielectrophoretic force in comparison with Coulomb force is less in factor R/r. In our case R/r ~ 4-8. As for as the force that acts in space charge occupied liquid, it seems there are no condition for it in these experiments.

Therefore Coulomb force is more suitable as source of bubble motion. The comparison of computed and experimentally measured elongation

is presented at fig. 8. Here it is chosen several series of bubble recording at cathode with the bubble r=27±5 mm at field strength 100 kV/cm. On fig.9 it is rectangular marks. Curve 1 is obtained as computation according bubble disharge model. Coincidence of marks and curve 1 is not very good. It is clear that some factor is absent in model. One should note that in model it is assumed bubble fully discharged bubble. It means that electric field in bubble after partial discharge equals zero. More realistic will be assumption that voltage across bubble will be supported at the level of breakdown voltage. In this case the surface charge past discharge in bubble is less approximately 1.5¸3 times. Figure depends on bubble size and field strength. More bubble and field - more surface charge.

One should obtain correction expression due to this circumstance. In formulae (11) surface charge will decrease

(13)

where U_p~300 V is Pashen's breakdown voltage. Equivalent pressure that moves bubble wall along field will decrease too

(14)

Computation of bubble's elongation according to corrected model is shown on fig. 8 as curve 2. Experimental marks well correspond to model.

As for as bubble's instability one can note a few moments. Bubbles divides on two bubbles in 5-10 ms. It is not contradict to expression (9). Low scaled observed disturbances have wavelengths at least 4-5 mm. Estimations according to (12) give 0.1 mm. If expression (12) change by analogy with (13), (14), the estimation of wavelength give 1-5 mm depending on electric field and bubble size. Only one result - bubble rest in form of wide cone on surface past anode bubble dividing have no proper explanation.

4 Conclusion

The behaviour of artificial micro-bubble at the action of electric stress is studied. The main factors are partial discharges in bubbles at electrical stresses that will lead to surface charge appearance, Coulomb forces, pressure increase and bubble elongation. Bubble instability should be at the time duration more than 5-10 ms approximately. In this experiments electric field is not enough for breakdown initiation in liquid before bubbles dividing.

Authors are grateful to RFBR and Ministry of Education for grants.

References

[1] Korobeynikov S.M. Deformation of bubbles in electric field. -Ingenerno-Physicheskii Journal, v.36, N5, pp.882-884, 1979 (in Russian).

[2] Korobeynikov S.M. Effect of electric field on boiling point. -Ingenerno-Physicheskii Journal, v.41, N6, pp.1131, 1981 (in Russian).

[3] Jones T.B., Bliss G.W. Bubble dielectrophoresis. -J. Appl. Phys., V.48, 4, p.1412-1417, 1977.

[4] S.M. Korobeinikov, “The Role of Bubbles in the Electric Breakdown of Liquids: Prebreakdown processes”, High Temperature. V. 36, No. 3, pp. 362–367, 1998.

[5] S. M. Korobeynikov, “The Role of Bubbles in the Electric Breakdown of Liquids: Comparison with Experiment”, High Temperature. V. 36, No. 4, pp. 517–523, 1998.

[6] I.Alexeff, M.O. Pace, T.V. Blalock and A.I. Winterberg. Possible Models for the Earliest Prebreakdown Events in DC Stressed Hexane. Conf. Record of 10 ICDL, Grenoble, France, pp.387-391.